Filtro de Kalman
Devido aos limites de coleta de dados presentes em alguns sistemas, nem todos os estados podem ser mesurados. Para tentar solucionar esse problema, é normal a utilização do que chamamos de estimadores de estados, que nada mais é do que uma ferramenta matemática para tentar reproduzir um sinal no qual um medidor não está apto a fazer, em outras palavras, o mesmo pode deduzir o que não pode ser medidos diretamente. A implementação do estimador pode ser utilizada num modelo linear utilizando uma ferramenta denominada de filtro de Kalman.
O filtro de Kalman é utilizado também para reduzir os efeitos gerados por ruídos que afetam o sistema. A junção da incerteza do sistema juntamente com a incerteza da sua modelagem é base para criar um estimador de estados que é capaz de reduzir tais efeitos. Dizemos então que o filtro de Kalman “limpa” o sinal de saída para ele se parecer ao máximo com um sinal hipotético sem ruído.
A implementação do filtro em simulações computacionais é feita através de um algoritmo desenvolvido pelo o Húngaro Rudolf Emil Kalman, figura importante na fundação do controle moderno, que atuava no campo da matemática e engenharia elétrica
A imagem acima descreve o diagrama de blocos do programa "Simulink" usado na implementação do filtro. Temos um modelo linear que recebe um ruido aleatório e que tem sua saída prejudicada. As matrizes A, B e C do sistema são utilizada para a construção do filtro, além do "ke", que é chamado de ganho de Kalman. Isso faz com que a "saída com" filtro tenha os efeitos do ruido amenizados. O ganho de kalman pode ser calculado com o seguinte algorítmo:
clear all
close all
clc
%Matrizes A e C
A=[0 1 0 0;-14.1873 0 57.4652 0;0 0 0 1;14.4888 0 -18.9635 0];
C =[1 0 0 0; 0 0 1 0;];
%Cálculo do Ke
R=0.01*eye(2);
Q=0.015*eye(4);
N=[0 0; 0 0; 0 0;0 0;];
G=eye(4);
[Ke,P,E] = lqe(A,G,C,Q,R,N)
%O valor de Ke é mostrado na área de trabalho
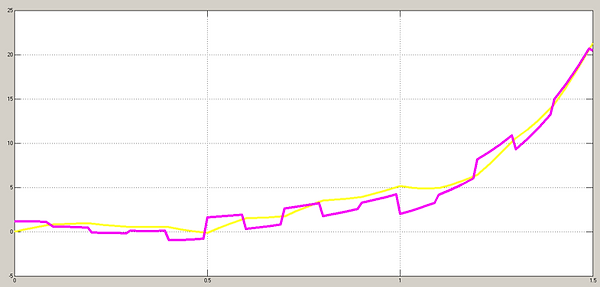
Veja os gráficos abaixo comprovando a eficacia do filtro nas duas saídas do sistema dos blocos mostrados anteriormente:
As linhas em roxo mostram as saídas do sistema com ruído e as linhas em amarelo mostram as mesmas com o filtro de Kalman. Os efeitos do ruído foram minimizados, tornando o sistema mais estável.